Sinespejo

El círculo A tiene un radio que es 1/3 del radio del círculo B. El círculo A se desplaza rotando a lo largo del perímetro de B hasta volver a su posición inicial. Cuando la alcance, cuántas vueltas completas habrá dado A?



A darle al coco... (al que vaya a contestar un consejo: no precipitarse)

Salu2!

En teoria 3, si no estoy equivocado, si la B no gira.

Ua propuesta:
Si cogemos la circunferencia de la tierra y le añadimos 1m, ¿en cuanto aumenta su radio? ¿y si hacemos lo mismo con una pelota de tenis?

Se ve que la fotografía ya no los entretiene...

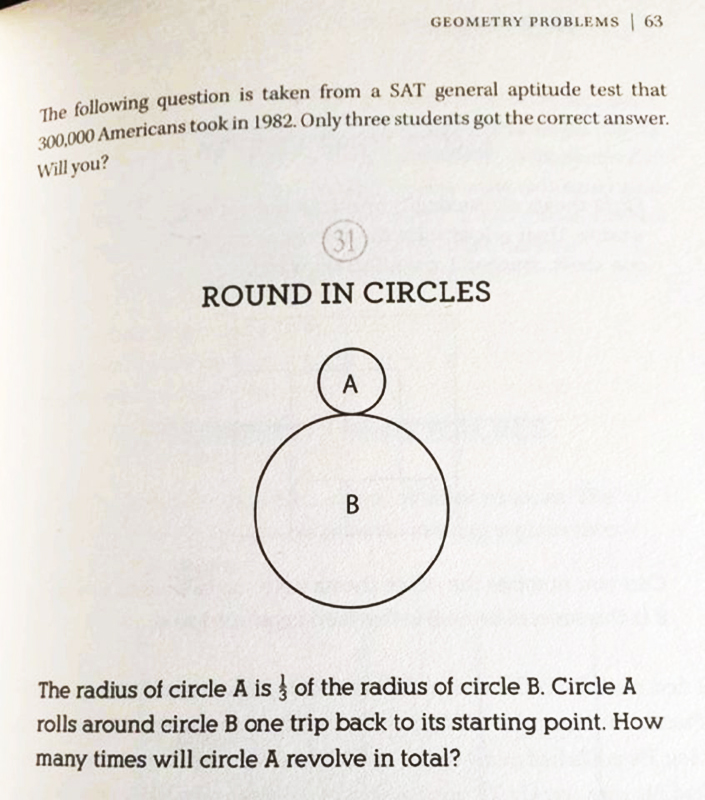
tonilluch escribió:En teoria 3, si no estoy equivocado, si la B no gira.

Ua propuesta:
Si cogemos la circunferencia de la tierra y le añadimos 1m, ¿en cuanto aumenta su radio? ¿y si hacemos lo mismo con una pelota de tenis?

Si el perímetro de una es 2πR y el de la otra 2π3R, y si una circunferencia dando una vuelta sobre sí misma recorre una distancia igual a su perímetro, parece obvio que el resultado debe ser 2π3R/2πR = 3.

Lo que no tiene sentido es que solo lo acertasen 3 personas de 300.000, cuando es la respuesta obvia. Así que igual hay truco, no sé.

EDITO: Tiene pinta de haber truco. Acabo de hacer la prueba con un taco de post-its y una moneda, y suponiendo que un lado del taco fuese igual al perímetro de la moneda, la moneda no necesita dar 4 vueltas sobre sí misma, como parecería normal, sino 5. Por la forma en la que se "desplaza" la moneda, cada vez que llega a un vértice necesita dar un cuarto de vuelta sobre sí misma a mayores (durante el que la superficie de la moneda no recorre ningún trayecto sobre el cuadrado), para colocarse en posición de recorrer el siguiente lado.

Así que sobre el círculo me da que le pasa lo mismo. Como con un triángulo me salen 4 vueltas y con un cuadrado 5, probablemente para el círculo sea también una más de las a priori necesarias: 4 vueltas.

marcuse escribió:Lo que no tiene sentido es que solo lo acertasen 3 personas de 300.000, cuando es la respuesta obvia. Así que igual hay truco, no sé.

No haría mucho caso de ese dato, es irrelevante. El test daba 5 posibles soluciones (que os he quitado por un buen motivo que desvelaré), así que por pura estadística sería improbabilísimo que de 300.000 solo 3 escogieran cualquiera de las opciones, hasta la más disparatada. Aunque solo fuera por error o cachondeo.

Salu2!

marcuse escribió:Acabo de hacer la prueba(...)

Lo siento pero la respuesta que te cuenta es la de 3

Salu2!

Es decir, las 3 propias del desarrollo lineal, y 1 más que es la vuelta por acompañamiento a la forma circular de la B, total 4 ¿sí?

JMLA escribió:Es decir, las 3 propias del desarrollo lineal, y 1 más que es la vuelta por acompañamiento a la forma circular de la B, total 4 ¿sí?

Así es. El círculo pequeño siempre hará tantas rotaciones sobre su centro como sea la relación de tamaños, más una que le sale de bonus por estar dando la vuelta al círculo grande. Aquí se marcan los momentos en que da cada vuelta para la relación de tamaños 3 del ejercicio:



Y la historia del examen, algo así como la Selectividad americana, es que las respuestas que daban eran erróneas (por eso os las quité, despistan más que ayudan), así que tuvieron que rectificar todas las notas por lo visto. Lo cuento aquí:

https://www.overfitting.net/2022/11/tes ... con-r.html

Salu2!

Hola, interesante y saludos de Felipe