[PÍLDORA 8] Geometría de las Vías Lácteas panorámicas
"Last week I was at about 10.000 feet with a clear, moonless sky, and a spectacular view of the summer Milky Way. To me it appeared to have a very pronounced curve. So I took the edge of a blanket, stretched it out taut, and held it up... and sure enough, the 'curve' is completely an optical illusion."
https://forum.cosmoquest.org/showthread ... ear-curved
______________
Fruto de varios debates en el foro sobre imágenes panorámicas de la Vía Láctea, me ha quedado claro que hay usuarios que pese a tener perfectamente dominada la técnica para obtener este tipo de panorámicas, tanto en cuanto a la captura como al posterior montaje, no tienen tan claro por qué sus imágenes muestran la Vía Láctea como un arco curvo que va de un punto a otro del horizonte:

Foto del forero FJS-MALAGA
GEOMETRÍA DE LA VÍA LÁCTEA
La Vía Láctea (VL) es una galaxia de tipo espiral de unos 100.000 años luz de diámetro, con el grueso de su contenido estelar situado en un mismo plano. El Sistema Solar, y por lo tanto la Tierra y el Sol, están sobre dicho plano y a unos 2/3 del centro de la galaxia. En otras palabras, si la VL fuera la provincia de Madrid nosotros viviríamos más o menos entre Pinto y Valdemoro:

CÓMO SE VE LA VÍA LÁCTEA DESDE LA TIERRA
En ciertas épocas del año y en zonas de baja contaminación lumínica, aunque sin la espectacularidad de las fotografías, la Vía Láctea es visible a simple vista alzando la mirada al cielo nocturno (yo solo he logrado verla aceptablemente en Formentera y en Albacete, en mitad de la nada). Y aquí empieza el lío: unos dicen creer verla de forma curva, acorde a como les sale en sus panorámicas, pero basta acudir a la geometría que hemos explicado para deducir que esto no es posible. Visto desde la Tierra, que está contenida en el plano principal de la galaxia, el grueso de estrellas formaría un anillo alrededor de nuestro planeta que por tanto veríamos como una acumulación lineal de estrellas.
Lo explicamos con un ejemplo: el hula hoop forma un arco cerrado, pero si te lo colocas alrededor de la cabeza y a la altura de los ojos como le pasa a este chaval, él solo puede ver una línea recta. Es cierto que puede ir girando su cabeza e irá viendo porciones nuevas del aro, lo que quizá le de una percepción de arco, pero mire en la dirección que mire siempre verá el trozo visible de hula hoop proyectado como una recta. Lo mismo le pasa a un observador que esté en la Tierra (chaval) al tratar de seguir con la vista la VL (hula hoop):

La VL vista en el cielo aparece por tanto como una nube aproximadamente lineal de estrellas que, por el amplio ángulo de visión que abarca (hasta 180º de hecho, solo limitado por el horizonte), requiere ir moviendo la cabeza para recorrerla con la mirada. Pero eso no hace que desde nuestra posición de observación esas estrellas dejen de contemplarse dispuestas de forma lineal, solo es una falsa noción de curvatura.
Y vamos un poco más allá: si en lugar de estar sobre la Tierra estuviésemos flotando en el espacio del Sistema Solar, veríamos 360º de Vía Lactea a nuestro alrededor, y se nos seguiría presentando como una alineación de estrellas porque estamos contenidos en ella. La diferencia respecto a estar en la Tierra sería que ahora podríamos girar hasta 360º en lugar de solo 180º, abarcando toda la VL:
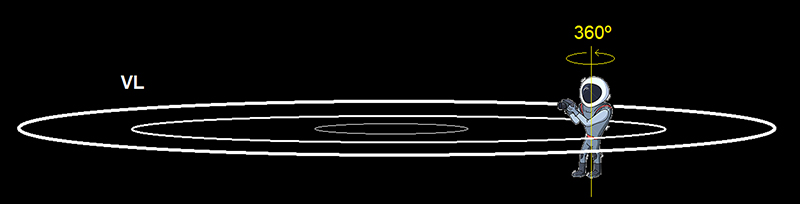
La Tierra en cambio es un (quasi) plano que nos limita ver como máximo ~180º de esos 360º, lo que a los fotógrafos de panorámicas de la VL les permite resolver fácilmente el montaje de la panorámica con una proyección cilíndrica.
EFECTO DE LA PROYECCIÓN CILÍNDRICA
Una proyección cilíndrica deforma, curvándolas como un arco, las líneas rectas que no coincidan con el ecuador de la panorámica. Lo vemos con un ejemplo lleno de referencias rectilíneas: ésta es la proyección cilíndrica de un restaurante abarcando un ángulo de visión de 180º:

Esa curvatura, que no existe en el mundo real, es la misma que aparece en las imágenes de la VL montadas con una panorámica de proyección cilíndrica. Pero pese a ese hándicap, es preciso usar este tipo de proyección ya que una proyección rectilínea (que no curvaría las líneas rectas) es inviable para un ángulo de visión cercano a 180º. Incluso para ángulos menores asequibles a una proyección rectilínea, el resultado deja de ser adecuado por la deformación (estiramiento) tan grande en los extremos (por convenio el máximo ángulo aceptable es de unos 120º). Puede verse la deformación y pérdida de calidad en los extremos:

Así que para fotografiar VL's que abarquen una parte importante de su recorrido lo mejor es usar una proyección cilíndrica (que probablemente será la que usen muchos programas sin siquiera preguntar al usuario). Este tipo de proyección permite componer un paisaje colocando el horizonte cerca del centro de la imagen, con lo que éste y los objetos que haya cerca de él saldrán sin deformación. Pero es bueno saber interpretar el resultado y darse cuenta de que la curva de la VL en la imagen final no es real sino fruto del proceso de proyección (SOFTWARE).
A no caer en la cuenta de esto ayuda que las VL se fotografían en plena naturaleza, alejadas de sujetos rectilíneos (calles, edificios) que delaten las deformaciones como el mobiliario del restaurante. En una pano de VL solo suele haber dos elementos rectilíneos en el mundo real: el horizonte (que seguirá saliendo rectilíneo si se coloca en el centro del recorrido de la pano, como es lo habitual) y la VL (que sí se curva como hemos visto). Para cualquier otro sujeto (montañas, árboles, piedras,...) la proyección cilíndrica funciona fantásticamente sacándolos con proporciones naturales y por eso es el tipo de proyección preferida en paisaje, no sólo en VL's.

Por lo tanto, e independientemente de cómo cada uno perciba la VL cuando mira para arriba (tanto si cree estar viendo un arco como si cree estar viendo una nebulosa rectilínea), lo que es objetivo y no admite discusión es que:
Si la VL en una imagen aparece como una curva -> es porque se aplicó una proyección no-rectilínea para generar esa imagen
CÓMO FOTOGRAFIAR TODA LA VL DE FORMA RECTILÍNEA AÚN CON UNA PROYECCIÓN NO RECTILÍNEA
Hay una forma de sacar toda la VL, que ésta quede como una recta, y sin sufrir la deformación en los extremos propia de la proyección rectilínea: se trata de hacer la pano precisamente rotando la cámara en el plano que contiene la VL, es decir seguir la VL allá donde se encuentre en el cielo desde su inicio en el horizonte hasta el otro extremo. En la imagen final la VL quedaría situada en el centro de la panorámica y por tanto la proyección cilíndrica (o cualquier proyección no-rectilínea que se use) no la curvaría, como no se curvaba la parte central de la imagen del restaurante. Los trozos de horizonte inicial y final de la VL aparecerán en la periferia de la imagen, y no será una imagen muy estética ni comprensible como paisaje nocturno, pero mostrará la VL tal y como se ve desde la Tierra.
Aquí se muestra como quedaría ese ejercicio con un ojo de pez que abarque prácticamente 180º:

Al pasar la VL por el centro de la imagen, cualquier deformación de la proyección del objetivo (una proyección de ojo de pez con simetría radial en este caso, no una cilíndrica) no la curva. En el momento en que esa foto no se hubiera hecho haciendo pasar la VL por el centro de la óptica, la proyección de ésta la habría curvado en forma de arco, más cuanto más se alejase del centro óptico. De hecho eso ha ocurrido con el horizonte, que se ha convertido en un círculo perfecto. Diríamos que mirando el horizonte al natural lo vemos como un arco curvo? o lo vemos recto (horizontal, de ahí su nombre)? pues lo mismo pasa con la VL.
FOTOGRAFIA DE 360º DE LA VL DE FORMA RECTILÍNEA
Para rizar el rizo, este astrónomo ha viajado a distintas partes del globo (South Africa, Texas y Michigan) para capturar toda la VL en un ángulo de 360º, lo equivalente al astronauta fotógrafo que vimos. Así ha logrado:

Entiendo que las partes más brillantes (centro) corresponden a la dirección de observación hacia el centro de la galaxia, donde mayor densidad de estrellas encontraremos (vimos que la Tierra dentro de la VL está situada de forma bastante periférica), y los tramos menos brillantes (extremos) corresponden a regiones de la VL aún más alejadas del centro que nuestro planeta, las que quedarían a espaldas del astronauta. Pero no tengo ni idea de si es así, nunca he hecho una foto de la VL.
En esta otra imagen puede verse el mismo tipo de imagen de la VL pero super detallada.
Salu2!
https://forum.cosmoquest.org/showthread ... ear-curved
______________
Fruto de varios debates en el foro sobre imágenes panorámicas de la Vía Láctea, me ha quedado claro que hay usuarios que pese a tener perfectamente dominada la técnica para obtener este tipo de panorámicas, tanto en cuanto a la captura como al posterior montaje, no tienen tan claro por qué sus imágenes muestran la Vía Láctea como un arco curvo que va de un punto a otro del horizonte:

Foto del forero FJS-MALAGA
GEOMETRÍA DE LA VÍA LÁCTEA
La Vía Láctea (VL) es una galaxia de tipo espiral de unos 100.000 años luz de diámetro, con el grueso de su contenido estelar situado en un mismo plano. El Sistema Solar, y por lo tanto la Tierra y el Sol, están sobre dicho plano y a unos 2/3 del centro de la galaxia. En otras palabras, si la VL fuera la provincia de Madrid nosotros viviríamos más o menos entre Pinto y Valdemoro:

CÓMO SE VE LA VÍA LÁCTEA DESDE LA TIERRA
En ciertas épocas del año y en zonas de baja contaminación lumínica, aunque sin la espectacularidad de las fotografías, la Vía Láctea es visible a simple vista alzando la mirada al cielo nocturno (yo solo he logrado verla aceptablemente en Formentera y en Albacete, en mitad de la nada). Y aquí empieza el lío: unos dicen creer verla de forma curva, acorde a como les sale en sus panorámicas, pero basta acudir a la geometría que hemos explicado para deducir que esto no es posible. Visto desde la Tierra, que está contenida en el plano principal de la galaxia, el grueso de estrellas formaría un anillo alrededor de nuestro planeta que por tanto veríamos como una acumulación lineal de estrellas.
Lo explicamos con un ejemplo: el hula hoop forma un arco cerrado, pero si te lo colocas alrededor de la cabeza y a la altura de los ojos como le pasa a este chaval, él solo puede ver una línea recta. Es cierto que puede ir girando su cabeza e irá viendo porciones nuevas del aro, lo que quizá le de una percepción de arco, pero mire en la dirección que mire siempre verá el trozo visible de hula hoop proyectado como una recta. Lo mismo le pasa a un observador que esté en la Tierra (chaval) al tratar de seguir con la vista la VL (hula hoop):

La VL vista en el cielo aparece por tanto como una nube aproximadamente lineal de estrellas que, por el amplio ángulo de visión que abarca (hasta 180º de hecho, solo limitado por el horizonte), requiere ir moviendo la cabeza para recorrerla con la mirada. Pero eso no hace que desde nuestra posición de observación esas estrellas dejen de contemplarse dispuestas de forma lineal, solo es una falsa noción de curvatura.
Y vamos un poco más allá: si en lugar de estar sobre la Tierra estuviésemos flotando en el espacio del Sistema Solar, veríamos 360º de Vía Lactea a nuestro alrededor, y se nos seguiría presentando como una alineación de estrellas porque estamos contenidos en ella. La diferencia respecto a estar en la Tierra sería que ahora podríamos girar hasta 360º en lugar de solo 180º, abarcando toda la VL:

La Tierra en cambio es un (quasi) plano que nos limita ver como máximo ~180º de esos 360º, lo que a los fotógrafos de panorámicas de la VL les permite resolver fácilmente el montaje de la panorámica con una proyección cilíndrica.
EFECTO DE LA PROYECCIÓN CILÍNDRICA
Una proyección cilíndrica deforma, curvándolas como un arco, las líneas rectas que no coincidan con el ecuador de la panorámica. Lo vemos con un ejemplo lleno de referencias rectilíneas: ésta es la proyección cilíndrica de un restaurante abarcando un ángulo de visión de 180º:

Esa curvatura, que no existe en el mundo real, es la misma que aparece en las imágenes de la VL montadas con una panorámica de proyección cilíndrica. Pero pese a ese hándicap, es preciso usar este tipo de proyección ya que una proyección rectilínea (que no curvaría las líneas rectas) es inviable para un ángulo de visión cercano a 180º. Incluso para ángulos menores asequibles a una proyección rectilínea, el resultado deja de ser adecuado por la deformación (estiramiento) tan grande en los extremos (por convenio el máximo ángulo aceptable es de unos 120º). Puede verse la deformación y pérdida de calidad en los extremos:

Así que para fotografiar VL's que abarquen una parte importante de su recorrido lo mejor es usar una proyección cilíndrica (que probablemente será la que usen muchos programas sin siquiera preguntar al usuario). Este tipo de proyección permite componer un paisaje colocando el horizonte cerca del centro de la imagen, con lo que éste y los objetos que haya cerca de él saldrán sin deformación. Pero es bueno saber interpretar el resultado y darse cuenta de que la curva de la VL en la imagen final no es real sino fruto del proceso de proyección (SOFTWARE).
A no caer en la cuenta de esto ayuda que las VL se fotografían en plena naturaleza, alejadas de sujetos rectilíneos (calles, edificios) que delaten las deformaciones como el mobiliario del restaurante. En una pano de VL solo suele haber dos elementos rectilíneos en el mundo real: el horizonte (que seguirá saliendo rectilíneo si se coloca en el centro del recorrido de la pano, como es lo habitual) y la VL (que sí se curva como hemos visto). Para cualquier otro sujeto (montañas, árboles, piedras,...) la proyección cilíndrica funciona fantásticamente sacándolos con proporciones naturales y por eso es el tipo de proyección preferida en paisaje, no sólo en VL's.

Por lo tanto, e independientemente de cómo cada uno perciba la VL cuando mira para arriba (tanto si cree estar viendo un arco como si cree estar viendo una nebulosa rectilínea), lo que es objetivo y no admite discusión es que:
Si la VL en una imagen aparece como una curva -> es porque se aplicó una proyección no-rectilínea para generar esa imagen
CÓMO FOTOGRAFIAR TODA LA VL DE FORMA RECTILÍNEA AÚN CON UNA PROYECCIÓN NO RECTILÍNEA
Hay una forma de sacar toda la VL, que ésta quede como una recta, y sin sufrir la deformación en los extremos propia de la proyección rectilínea: se trata de hacer la pano precisamente rotando la cámara en el plano que contiene la VL, es decir seguir la VL allá donde se encuentre en el cielo desde su inicio en el horizonte hasta el otro extremo. En la imagen final la VL quedaría situada en el centro de la panorámica y por tanto la proyección cilíndrica (o cualquier proyección no-rectilínea que se use) no la curvaría, como no se curvaba la parte central de la imagen del restaurante. Los trozos de horizonte inicial y final de la VL aparecerán en la periferia de la imagen, y no será una imagen muy estética ni comprensible como paisaje nocturno, pero mostrará la VL tal y como se ve desde la Tierra.
Aquí se muestra como quedaría ese ejercicio con un ojo de pez que abarque prácticamente 180º:

Al pasar la VL por el centro de la imagen, cualquier deformación de la proyección del objetivo (una proyección de ojo de pez con simetría radial en este caso, no una cilíndrica) no la curva. En el momento en que esa foto no se hubiera hecho haciendo pasar la VL por el centro de la óptica, la proyección de ésta la habría curvado en forma de arco, más cuanto más se alejase del centro óptico. De hecho eso ha ocurrido con el horizonte, que se ha convertido en un círculo perfecto. Diríamos que mirando el horizonte al natural lo vemos como un arco curvo? o lo vemos recto (horizontal, de ahí su nombre)? pues lo mismo pasa con la VL.
FOTOGRAFIA DE 360º DE LA VL DE FORMA RECTILÍNEA
Para rizar el rizo, este astrónomo ha viajado a distintas partes del globo (South Africa, Texas y Michigan) para capturar toda la VL en un ángulo de 360º, lo equivalente al astronauta fotógrafo que vimos. Así ha logrado:
- Obtener la VL al completo proyectándola con forma rectilínea pero usando una proyección cilíndrica que no estire ninguna parte de la panorámica.
- No incluir el horizonte por ser una panorámica de 360º solo del cielo, cuyo extremo derecho empalmaría con el izquierdo (componerla contra un paisaje obviamente le importaba un pito al autor, es una fotografía más científica que artística).

Entiendo que las partes más brillantes (centro) corresponden a la dirección de observación hacia el centro de la galaxia, donde mayor densidad de estrellas encontraremos (vimos que la Tierra dentro de la VL está situada de forma bastante periférica), y los tramos menos brillantes (extremos) corresponden a regiones de la VL aún más alejadas del centro que nuestro planeta, las que quedarían a espaldas del astronauta. Pero no tengo ni idea de si es así, nunca he hecho una foto de la VL.
En esta otra imagen puede verse el mismo tipo de imagen de la VL pero super detallada.
Salu2!







