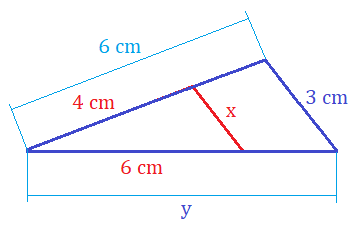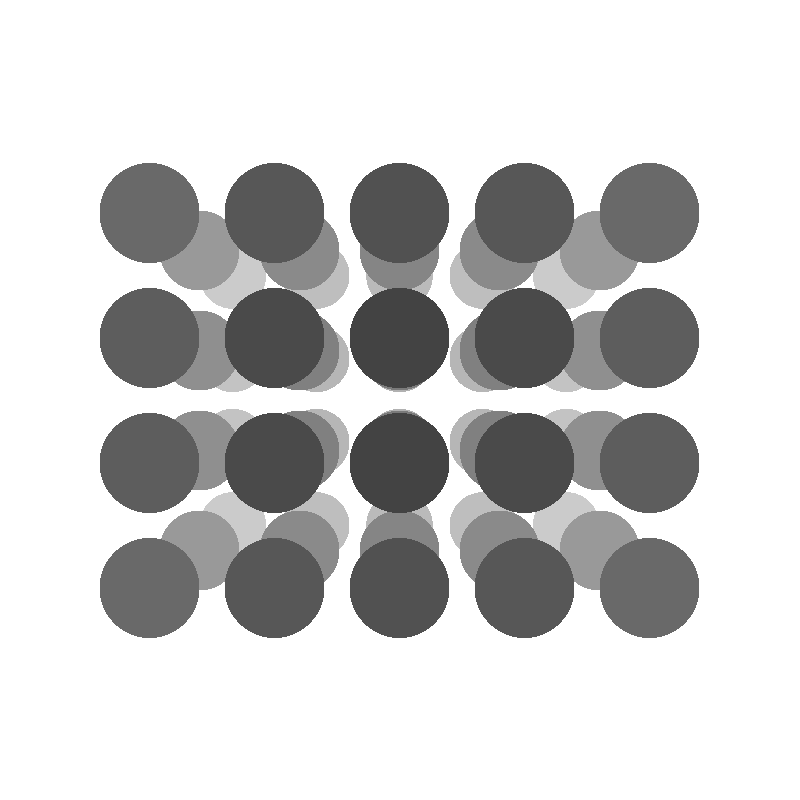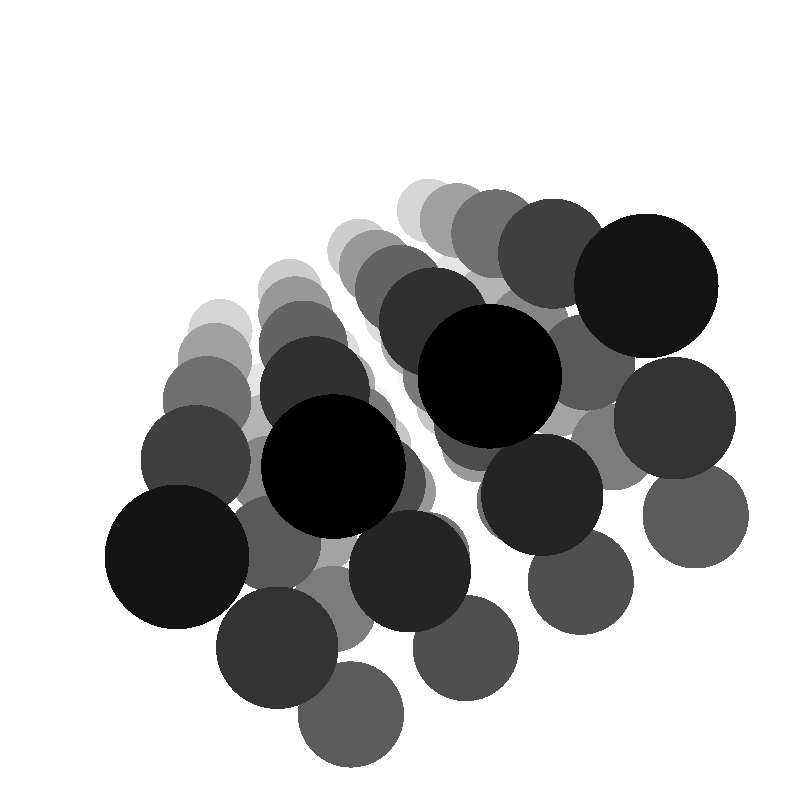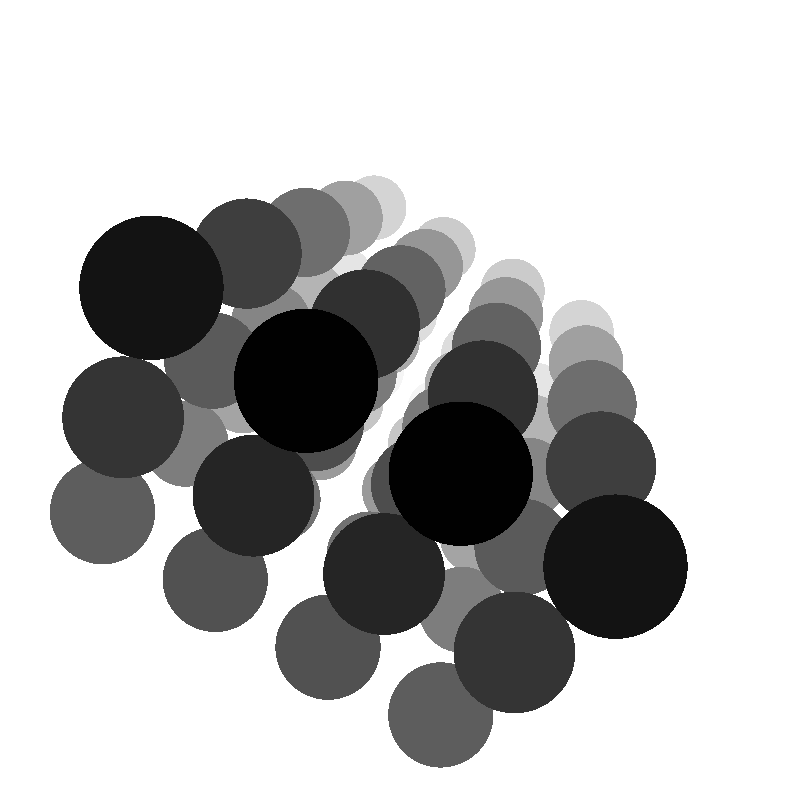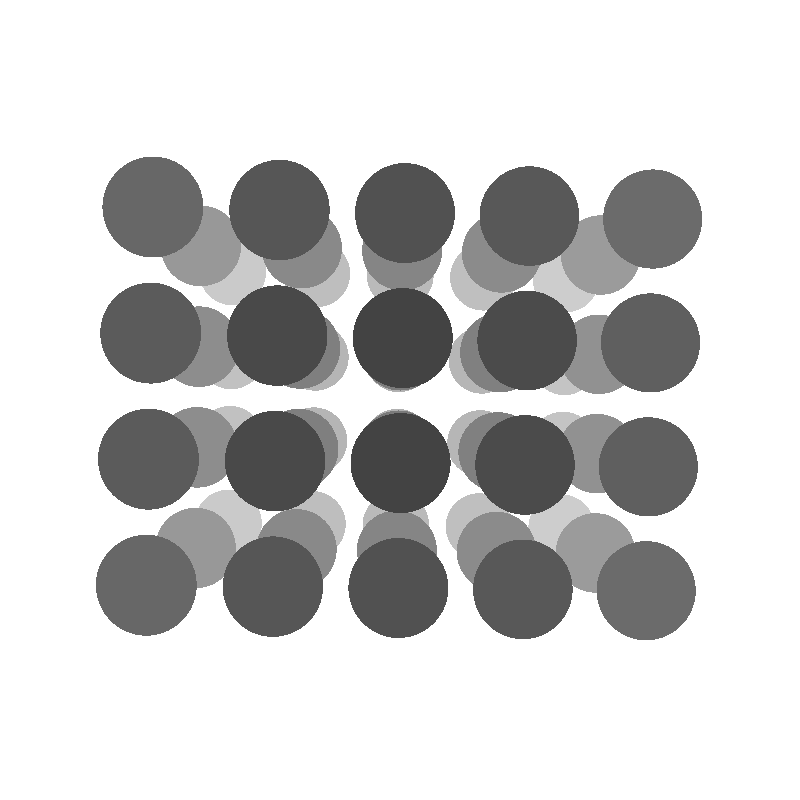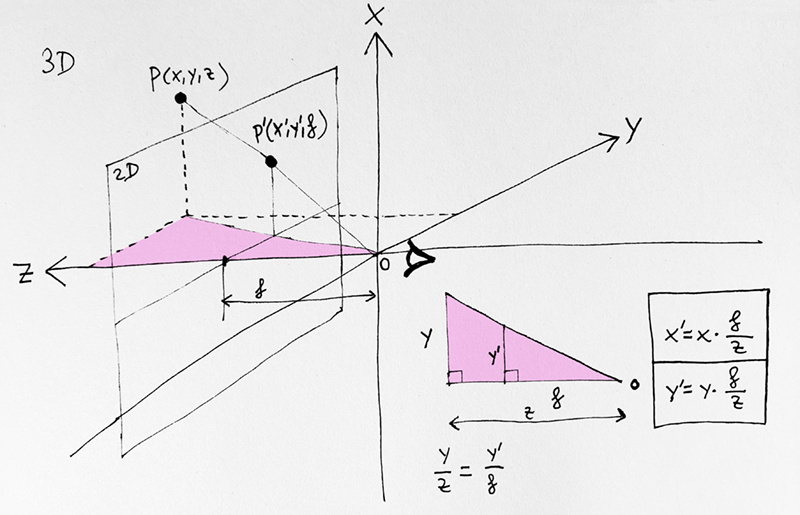
Asumiendo que nuestro punto de observación es el origen de coordenadas y miramos en la dirección del eje Z, un punto P definido por sus coordenadas (x,y,z) en el espacio 3D se proyecta sobre el plano de distancia focal f como el punto P' de coordenadas (x',y',f). La obtención de los valores x' e y' es tan inmediata como expresa la fórmula: ambos quedan reducidos por el factor f/z que es la relación entre la distancia f del plano de proyección (distancia focal del objetivo) y la distancia z que hay entre el observador (cámara) y el punto (sujeto).
Esta relación f/z es sumamente interesante para entender el efecto de la distancia focal (f) y la distancia al sujeto (z) en fotografía:
- Alterar f, es decir desplazar el plano de proyección, solo modifica el escalado o ángulo de visión de la escena porque afecta por igual a todos los puntos de la misma. Es equivalente a hacer un escalado o zoom de la imagen pero no modifica las relaciones de tamaño entre objetos, es decir no modifica la perspectiva.
- En cambio al ser z un valor diferente en función de la distancia entre la cámara y cada elemento de la escena, sí determinará la perspectiva de la imagen obtenida. Cuando z tiende a infinito (sujetos muy lejanos), el factor f/z será aproximadamente el mismo para todos los puntos de la escena obteniendo el equivalente a una perspectiva axonométrica (lo que los fotógrafos llaman "compresión de planos").
Otra lectura que se obtiene intuitivamente del esquema, es que cualquier objeto que tenga forma de línea recta en el mundo real se proyectará también como una recta en el plano (distorsiones de barril/cojín de una óptica al margen). De hecho ni siquiera tiene que ser un objeto realmente rectilíneo, basta que se presente como tal desde el punto de vista del observador (por ejemplo la Vía Láctea pese a ser una espiral de estrellas, desde nuestro planeta se ve como una alineación lineal de estrellas al estar la Tierra contenida en ella y por eso la capturamos como una recta de estrellas, mal que le pese a muchos fotógrafos de nocturnas que la prefieren representar como un arco).
Con esas simples ecuaciones he construido una animación con esferas (cuyo radio se escala por el mismo factor f/z que la localización de su centro). He escogido un ejemplo con esferas porque tienen una propiedad que me apetecía explotar. Si proyectar objetos 3D sobre un plano es tan sencillo como he explicado, detectar qué objetos tapan o intersecan a otros es en cambio sumamente complicado. A día de hoy los algoritmos ya están trilladísimos y muy bien implementados, incluso por hardware, en cualquier programa de animación 3D, arquitectura o videojuego. Pero con las esferas tengo un algoritmo de eliminación de partes ocultas tan sencillo como es dibujarlas por orden, de mayor a menor distancia al observador. Así las que estén más cerca ocultarán a las que están más lejos y el resultado es equivalente a un algoritmo real mucho más complejo:
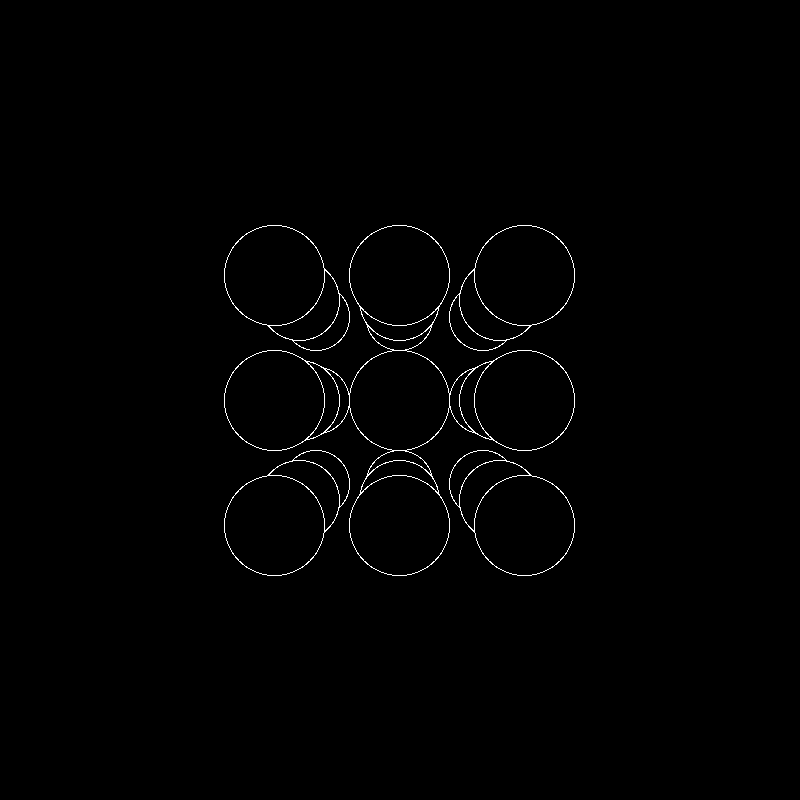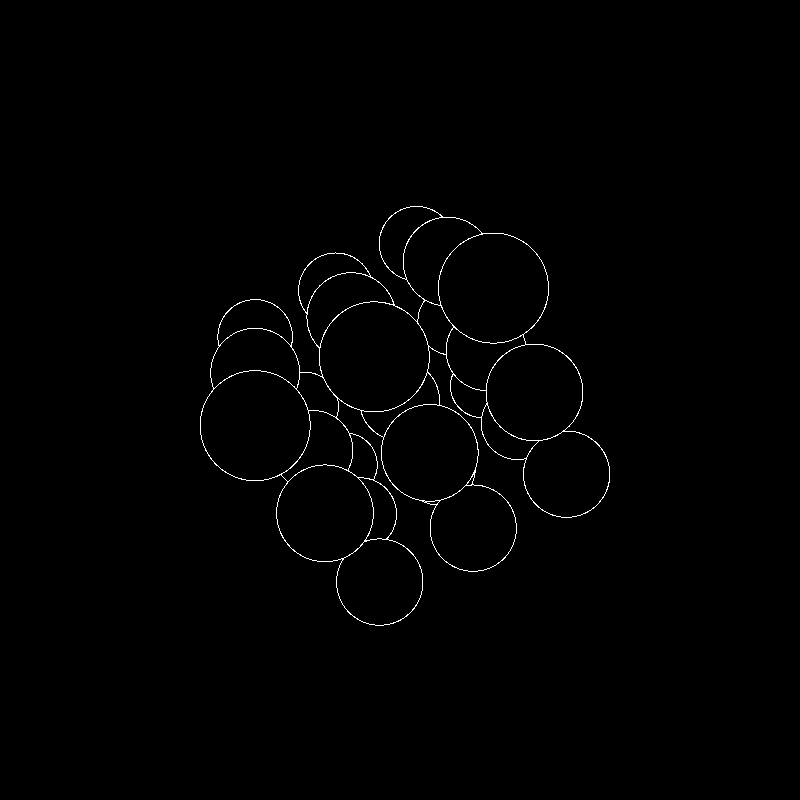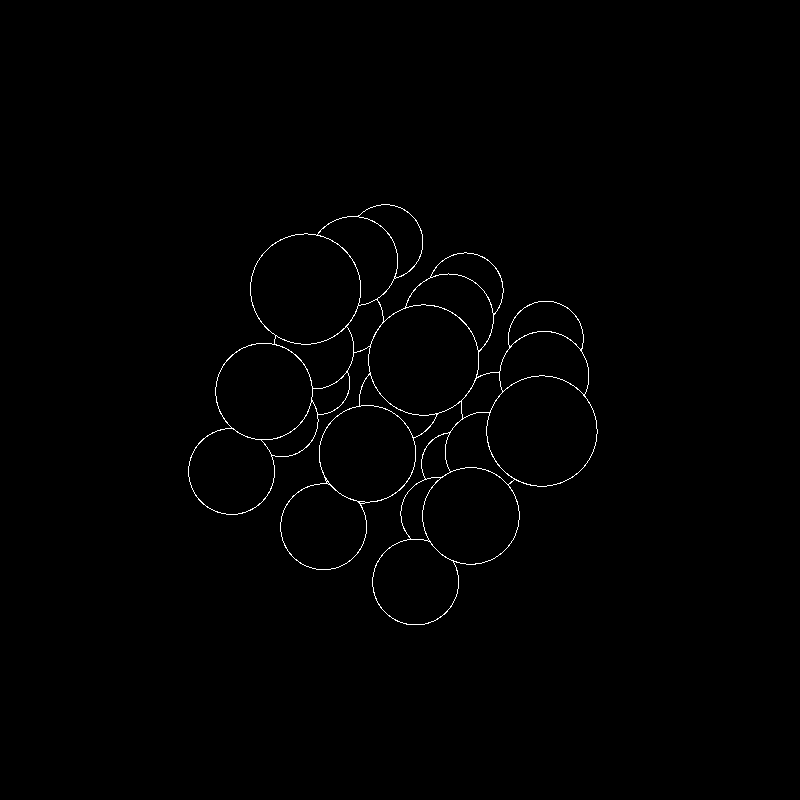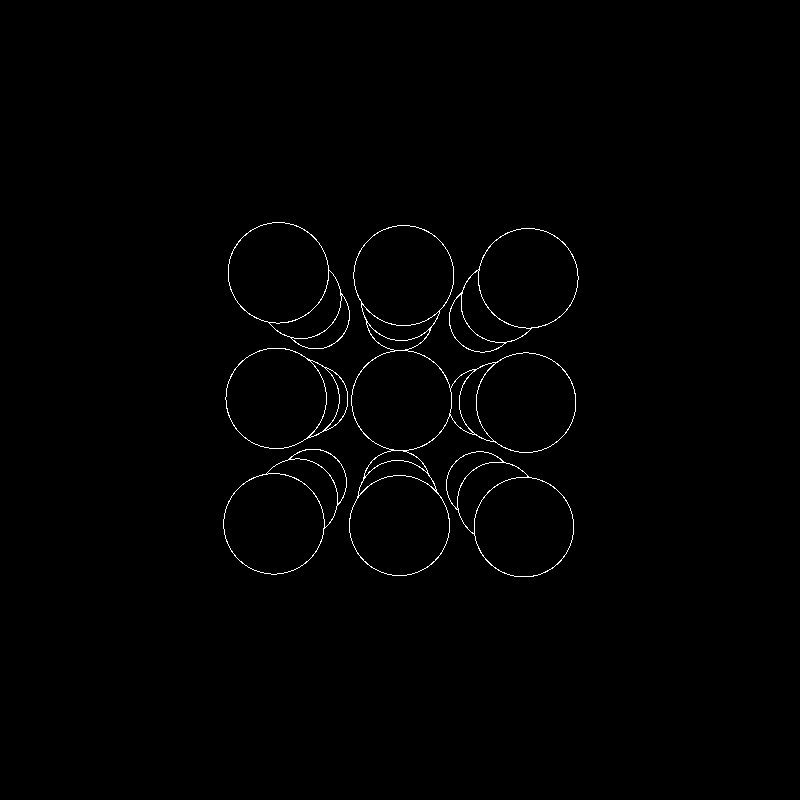
Aquí una versión coloreando las esferas con un tono de gris proporcional a la distancia al observador para crear un efecto de profundidad aérea:
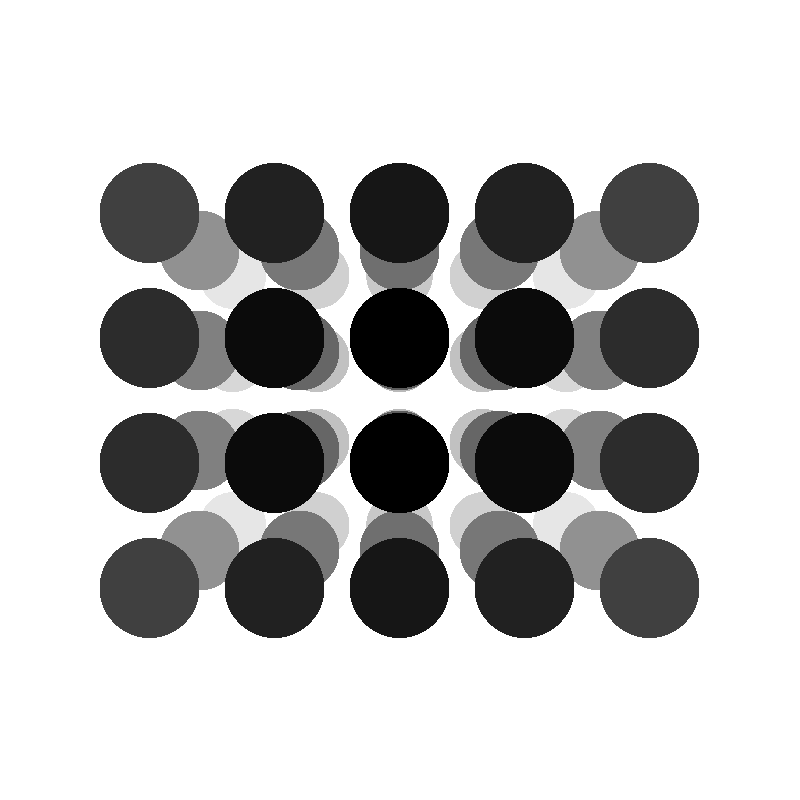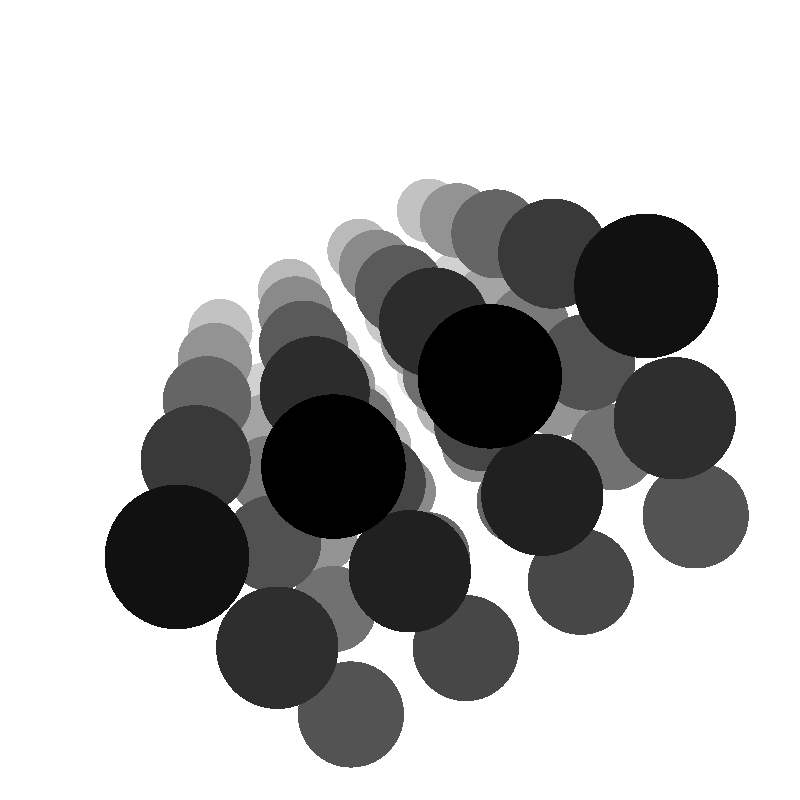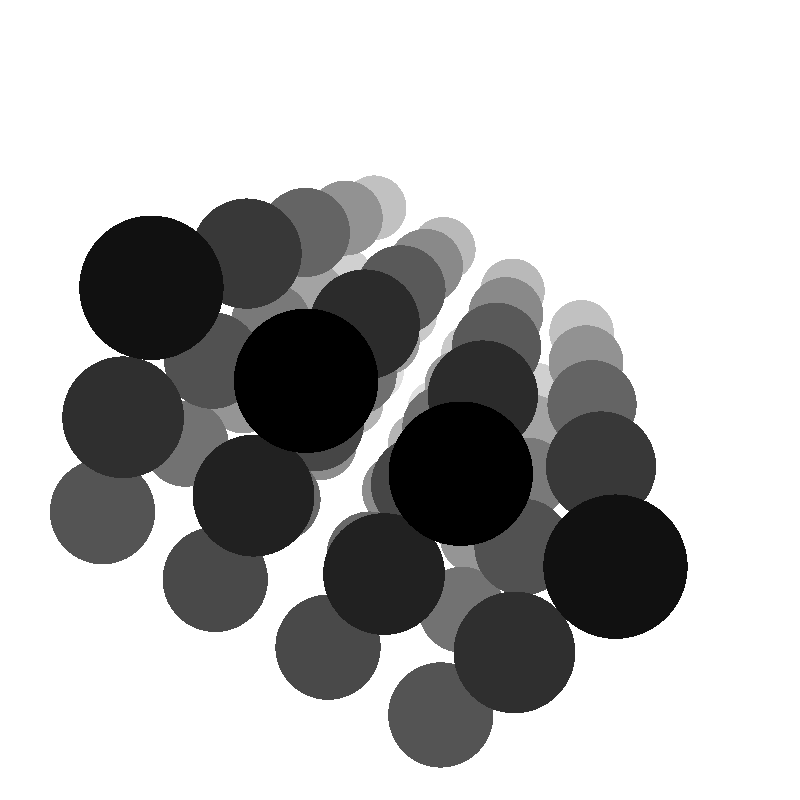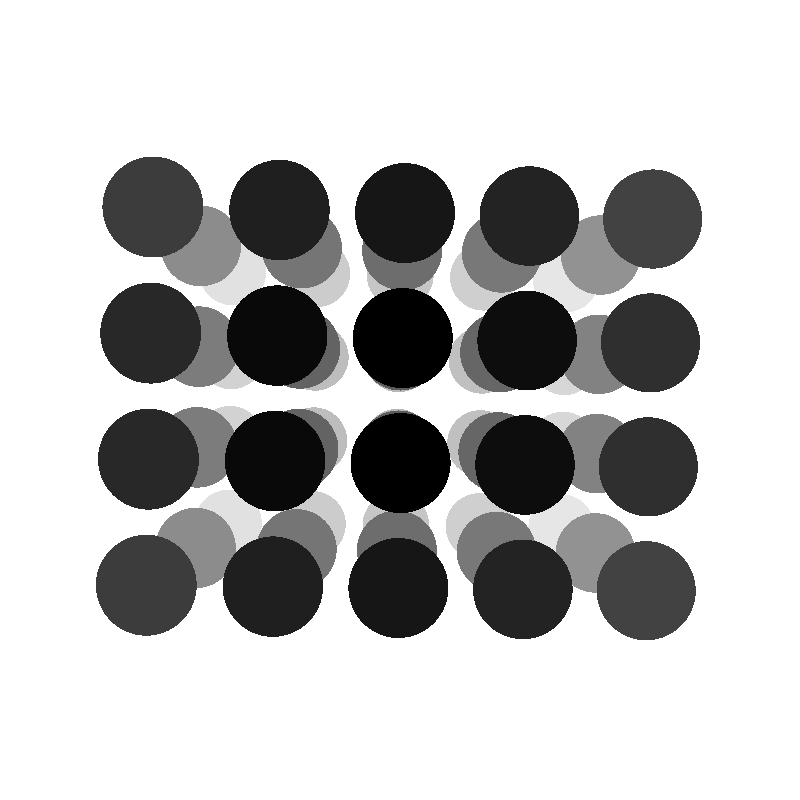
Salu2!
a si le damos al bolo nos entretenemos y combatimos el alzeimer que los que tenemos ya una edad.... 
