Parece que ni mi voto por la opción 1 os ha disuadido de votar la opción 2
No sé si se entendía del todo lo que preguntaba: no era si haciendo la media de dos capturas iguales se reduce el ruido, algo que es de sobra conocido, sino si puede reducirse el ruido aún
cuando una de las 2 captura es claramente más ruidosa que la otra. Puede resultar contraintuitivo: cómo va una imagen llena de grano a ayudar a limpiar otra que está más limpia?.
La realidad es que por mucho ruido que tenga la imagen más ruidosa, siempre puede contribuir a hacer el resultado más limpio. Si la diferencia de ruido entre las dos imágenes es muy grande la contribución de la ruidosa tenderá a 0, pero nunca será nula.
He calculado que si la relación entre el ruido de las imágenes 1 y 2 es k:
Ruido_1 = k * Ruido_2 (0 < k < oo)
O dicho de otro modo, si:
Relación S/N_1 = 1/k * Relación S/N_2La máxima mejora al fusionar ambas imágenes se consigue con un parámetro de transparencia:
alpha_optimo = 1 / (k^2 + 1) (0 < alpha_optimo < 1)
En el ejemplo que he construido con ruido gaussiano puro, la diferencia de ruido la he tomado de k=1,66666..., lo que da un alpha_optimo = 26,47% de transparencia para la imagen ruidosa, y por tanto un 73,53% para la menos ruidosa. Cuando me he llevado las imágenes a Photoshop, el cálculo ha sido casi perfecto (con ruido siempre hay una incertidumbre): para una fusión con transparencia 73% (Photoshop no deja decimales) se tiene la máxima relación S/N en la fusión; aumentando o disminuyendo empeora. La mejora no es para tirar cohetes pero menos da una piedra:
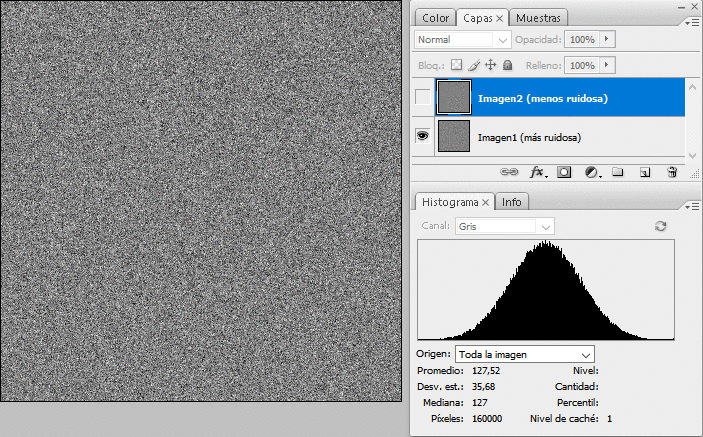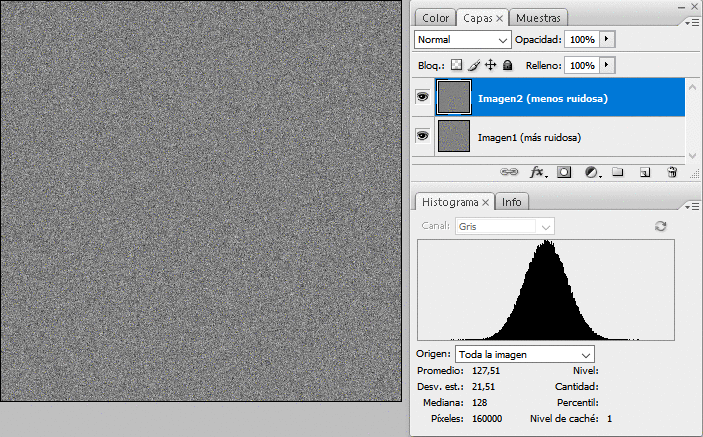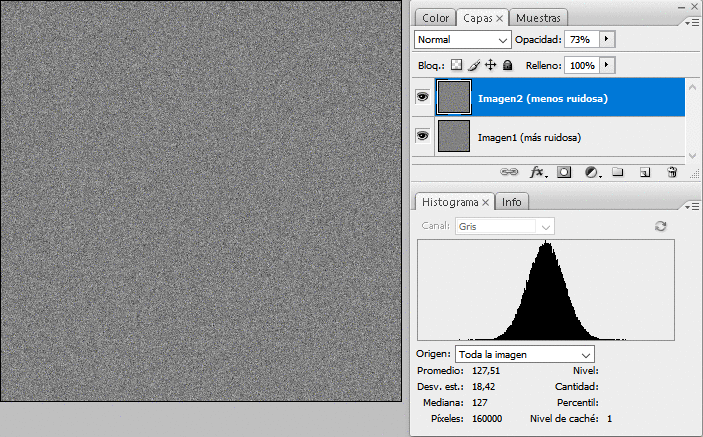
La animación muestra la imagen 1 (la más ruidosa), luego la 2 (la menos ruidosa) y por último la fusión óptima (el estrechamiento del histograma desde la imagen 2 es la contribución a la reducción del ruido de la imagen 1).
En esta gráfica puede verse que ninguna otra fusión habría dado una imagen menos ruidosa (cuando más varianza, más ruido y peor relación S/N): a la izquierda sería tomar solo la imagen 2, en el centro sería hacer una fusión 50%/50% (la habitual que hace casi todo el mundo, y que de hecho es el alpha_optimo cuando ambas imágenes tienen el mismo ruido):
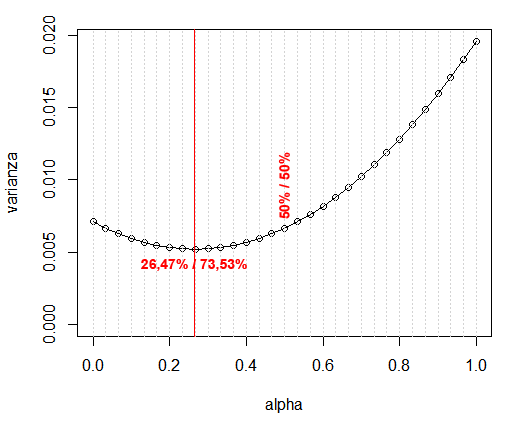
La fórmula de alpha_optimo no me la he sacado de la manga, un poco de estadística y se deduce:
Que para qué sirve esto? en aplicaciones normales para nada desde luego. Pero en programas de HDR (donde hay capturas de diferente relación S/N que hay que fusionar), o en astrofotografía donde se tiene que afinar todo lo posible puede tener aplicación. A mí me ha venido genial para practicar con un lenguaje que estoy aprendiendo.
El código:
- Código: Seleccionar todo
LARGO=160000
FINE=31L
SD1=0.04*3.5
SD2=0.024*3.5
k=SD1/SD2
alphaopt=1/(k^2+1) # alpha que maximiza la S/N de la mezcla
mejora_N1=(k^2+1)^0.5
mejora_N2=(1/(k^2)+1)^0.5
S1=seq(from=0.5, to=0.5, len=LARGO)
N1=rnorm(LARGO, mean=0, sd=SD1)
S2=S1
N2=rnorm(LARGO, mean=0, sd=SD2)
# xaxis=seq(from=0, to=1, len=LARGO)
# plot(xaxis, S1+N1, ylim=c(0,1) , type='l')
# plot(xaxis, S2+N2, ylim=c(0,1) , type='l')
alpha=as.array(seq(from=0, to=1, len=FINE))
y=array(0, dim=c(FINE,LARGO))
for (i in 1:FINE) y[i,]=alpha[i]*(S1+N1)+(1-alpha[i])*(S2+N2)
yopt=alphaopt*(S1+N1)+(1-alphaopt)*(S2+N2)
varianza=alpha
for (i in 1:FINE) varianza[i]=var(y[i,])
plot(alpha, varianza, ylim=c(0,max(var(N1),var(N2))), type='o')
abline(v=alphaopt, col='red')
abline(v=alpha, col="lightgray", lty = "dotted")
# Checks
SNR1=mean(S1)/(var(N1)^0.5)
SNR2=mean(S2)/(var(N2)^0.5)
SNRopt=mean(yopt)/(var(yopt)^0.5)
print(paste0("SNRopt/SNR1=", round(SNRopt/SNR1, digits=4)," vs mejora_N1=",
round(mejora_N1,4)))
print(paste0("SNRopt/SNR2=", round(SNRopt/SNR2, digits=4)," vs mejora_N2=",
round(mejora_N2,4)))
img1=as.array(S1+N1)
img2=as.array(S2+N2)
imgout=as.array(yopt)
dim(img1) <- c(400,400) # Genialidad para convertir un vector en imagen
dim(img2) <- c(400,400)
dim(imgout) <- c(400,400)
# library(grid)
# grid.raster(imagen-min(imagen))
hist(img1, breaks=200, xlim=0:1)
img1[img1 < 0] <- 0
img2[img1 < 0] <- 0
imgout[imgout < 0] <- 0
img1[img1 > 1] <- 1
img2[img2 > 1] <- 1
imgout[imgout > 1] <- 1
library(tiff)
writeTIFF(img1, "img1.tif", bits.per.sample=16, compression="LZW")
writeTIFF(img2, "img2.tif", bits.per.sample=16, compression="LZW")
writeTIFF(imgout, "imgout.tif", bits.per.sample=16, compression="LZW")
Salu2!
Publicado: Lun Mar 27, 2017 12:56 am
si la foto es la misma el ruido está correlado ya que es exactamente el mismo, y por lo tanto no hay mejora de relación S/N, (A+A)/2=A. Si miras las fórmulas verás que hay un término de Covarianza que solo vale 0 si el ruido está incorrelado.
