
Virtualmente la esfera refleja cualquier cosa que no oculte a la cámara la propia esfera, aunque en la periferia de la bola la compresión de ángulos de entrada es tal que difícilmente se podrá obtener información útil. En el anterior ejemplo la única parte de la habitación que no aparece reflejada en la esfera es la pequeña porción del trapo verde que queda detrás de la misma, por eso todo el perímetro de la esfera se ve verde ya que refleja trapo. Yo me tuve que salir de la habitación o no tenía forma de no salir en la foto. Esto implica un ángulo de visión enorme (más cercano a 360º cuanto más pequeña sea la esfera y más alejada esté la cámara):
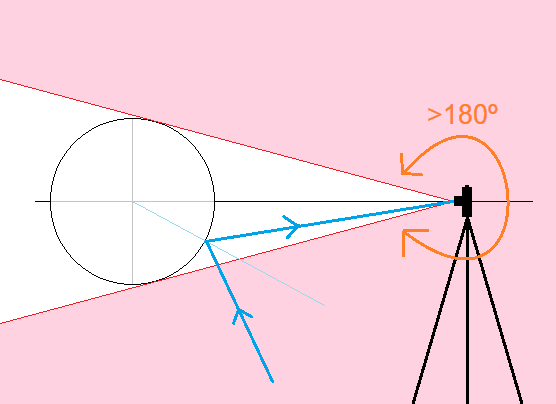
La segunda parte del ejercicio, y el motivo real por el que lo quiero hacer, es calcular la corrección de la captura con fuerte deformación tipo ojo de pez para hacerla rectilínea. Por supuesto no se puede corregir a rectilíneo todo lo que refleja la esfera, solo podemos aspirar a convertir en rectilíneo un ángulo inferior a 180º (es decir, un círculo interior del total que refleja la esfera por ejemplo).
Con las primeras pruebas ya me he dado cuenta de dos cosas:
- La esfera metálica que tenía en la oficina y que me regaló no sequién, de unos 35mm de diámetro, aunque en mano parece un espejo decente es una castaña: demasiado pequeña, con una superficie muy poco regular y pulida, y encima llena de rayaduras. Así que he pedido otra por Amazon de 100mm de diámetro que por lo menos no estará rayada y espero de más calidad. He usado un objetivo macro para cubrir toda la vertical del sensor M4/3. Con la de 100mm espero poder usar alguno de mis objetivos FF en la A7.
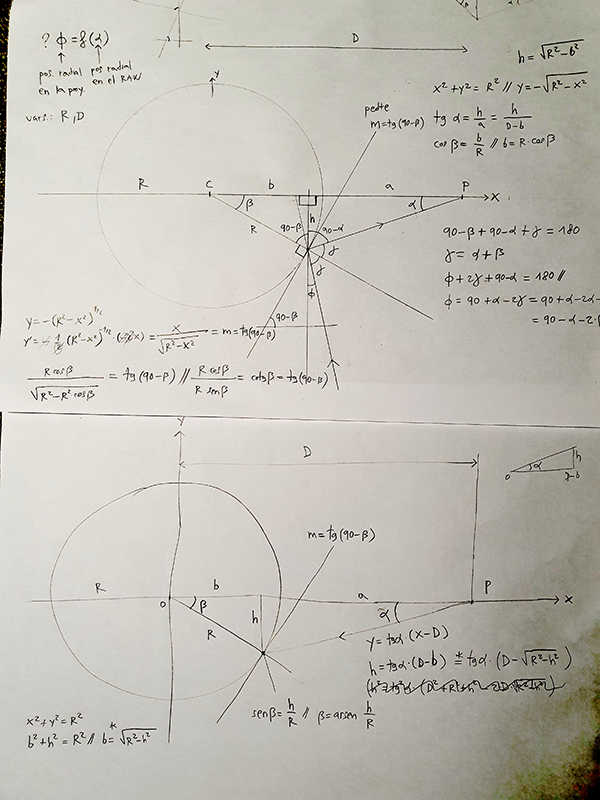
- A priori pensé que obtener las ecuaciones exactas para realizar la corrección de la proyección que hace la esfera a una rectilínea sería sencillo y saldrían ecuaciones limpias, porque la geometría es básica. La realidad es que no es para nada así, he llegado a una ecuación que debe resolverse por fuerza bruta usando métodos numéricos para cada ángulo de incidencia, así que va a costar un poco pero espero lograrlo.
Si alguna vez habéis tenido en la mano alguna de estas esferas (una bola de Navidad por ejemplo), son bastante curiosas y si uno se fija se pueden aprender cosas sobre óptica, proyecciones y formas de lograr ángulos de visión extremos. Escher dibujó una muy popular, supongo que copió del natural porque sino vaya crack:

Por las propiedades vistas si uno pone una esfera de éstas al sol, se debería ver como un objeto brillante desde cualquier dirección del espacio desde la que se la mire, ya que siempre habrá una parte de la superficie de la misma que refleje el sol en la dirección de observación.
Salu2!
