Fecha actual Sab Mar 07, 2026 1:50 pm
[ENCUESTA] Ruido al mezclar dos imágenes
Moderadores: IOM60, laucsap60, klomp, Siniestro, Guillermo Luijk, Pablo Valido
25 mensajes
• Página 1 de 1
[ENCUESTA] Ruido al mezclar dos imágenes
Una encuesta para ver lo que intuitivamente pensáis: si tenemos dos capturas de una misma escena, una con más ruido que la otra (por ejemplo porque se obtuvo con menor exposición), podemos de algún modo obtener una imagen final con menos ruido que eligiendo simplemente la captura que individualmente tiene menos ruido?.
Pista: si hacemos dos capturas de una misma escena con los mismos parámetros, hay algo que suele hacerse para obtener una imagen final con menos ruido que el que presentan ambas capturas?.
Para votar hay que entrar por web.
Salu2!
Pista: si hacemos dos capturas de una misma escena con los mismos parámetros, hay algo que suele hacerse para obtener una imagen final con menos ruido que el que presentan ambas capturas?.
Para votar hay que entrar por web.
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
En astrofotografia se hace mucho, y tiene su logica.
SoyElTroll
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
-

soyeltroll - Mensajes: 2838
- Registrado: Lun Jul 02, 2012 12:45 am
- Ubicación: Valencia
Re: [ENCUESTA] Ruido al mezclar dos imágenes
A mi me gustarla saber como se hace.
-

Pau - Mensajes: 7450
- Registrado: Lun Dic 29, 2014 7:33 pm
- Ubicación: Vulcano
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Me uno a Pau, también me gustaría saber como se hace!
saludos
saludos
a7rii / Olympus Om2n
Sony Zeiss 16 35 F4 FE.
Voigtlander 50mm F2 Apo-Lanthar FE
Canon EF 70 200 F4 L
Helios 44m-2 m42
https://www.flickr.com/photos/alfon80/
Sony Zeiss 16 35 F4 FE.
Voigtlander 50mm F2 Apo-Lanthar FE
Canon EF 70 200 F4 L
Helios 44m-2 m42
https://www.flickr.com/photos/alfon80/
-

Alfon80 - Mensajes: 1031
- Registrado: Mié Ene 20, 2016 8:32 pm
- Ubicación: En un lugar de la Mancha.
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Pau escribió:A mi me gustarla saber como se hace.
Alfon80 escribió:Me uno a Pau, también me gustaría saber como se hace!
saludos
http://www.lonelyspeck.com/milky-way-ex ... photoshop/
[youtube]http://www.youtube.com/watch?v=zzVSm64zq44[/youtube]
-

toshiro - Mensajes: 3348
- Registrado: Vie Nov 11, 2011 1:00 pm
- Ubicación: Compostela
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Muchas gracias compi!
Enviado desde mi iPhone utilizando Tapatalk
Enviado desde mi iPhone utilizando Tapatalk
a7rii / Olympus Om2n
Sony Zeiss 16 35 F4 FE.
Voigtlander 50mm F2 Apo-Lanthar FE
Canon EF 70 200 F4 L
Helios 44m-2 m42
https://www.flickr.com/photos/alfon80/
Sony Zeiss 16 35 F4 FE.
Voigtlander 50mm F2 Apo-Lanthar FE
Canon EF 70 200 F4 L
Helios 44m-2 m42
https://www.flickr.com/photos/alfon80/
-

Alfon80 - Mensajes: 1031
- Registrado: Mié Ene 20, 2016 8:32 pm
- Ubicación: En un lugar de la Mancha.
alpha_optimo
Parece que ni mi voto por la opción 1 os ha disuadido de votar la opción 2 
No sé si se entendía del todo lo que preguntaba: no era si haciendo la media de dos capturas iguales se reduce el ruido, algo que es de sobra conocido, sino si puede reducirse el ruido aún cuando una de las 2 captura es claramente más ruidosa que la otra. Puede resultar contraintuitivo: cómo va una imagen llena de grano a ayudar a limpiar otra que está más limpia?.
La realidad es que por mucho ruido que tenga la imagen más ruidosa, siempre puede contribuir a hacer el resultado más limpio. Si la diferencia de ruido entre las dos imágenes es muy grande la contribución de la ruidosa tenderá a 0, pero nunca será nula.
He calculado que si la relación entre el ruido de las imágenes 1 y 2 es k:
Ruido_1 = k * Ruido_2 (0 < k < oo)
O dicho de otro modo, si:
Relación S/N_1 = 1/k * Relación S/N_2
La máxima mejora al fusionar ambas imágenes se consigue con un parámetro de transparencia:
alpha_optimo = 1 / (k^2 + 1) (0 < alpha_optimo < 1)
En el ejemplo que he construido con ruido gaussiano puro, la diferencia de ruido la he tomado de k=1,66666..., lo que da un alpha_optimo = 26,47% de transparencia para la imagen ruidosa, y por tanto un 73,53% para la menos ruidosa. Cuando me he llevado las imágenes a Photoshop, el cálculo ha sido casi perfecto (con ruido siempre hay una incertidumbre): para una fusión con transparencia 73% (Photoshop no deja decimales) se tiene la máxima relación S/N en la fusión; aumentando o disminuyendo empeora. La mejora no es para tirar cohetes pero menos da una piedra:
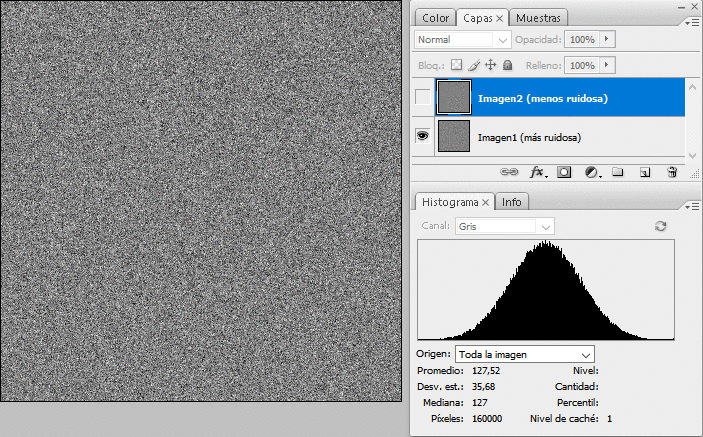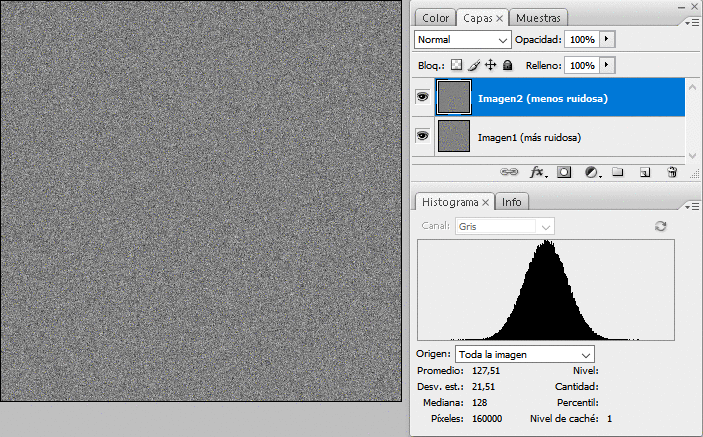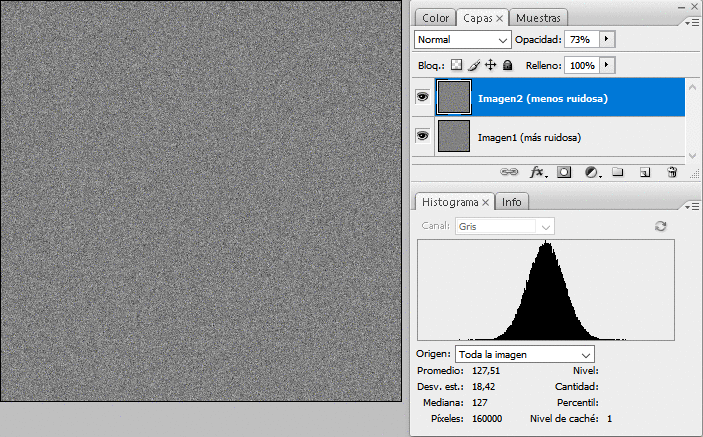
La animación muestra la imagen 1 (la más ruidosa), luego la 2 (la menos ruidosa) y por último la fusión óptima (el estrechamiento del histograma desde la imagen 2 es la contribución a la reducción del ruido de la imagen 1).
En esta gráfica puede verse que ninguna otra fusión habría dado una imagen menos ruidosa (cuando más varianza, más ruido y peor relación S/N): a la izquierda sería tomar solo la imagen 2, en el centro sería hacer una fusión 50%/50% (la habitual que hace casi todo el mundo, y que de hecho es el alpha_optimo cuando ambas imágenes tienen el mismo ruido):
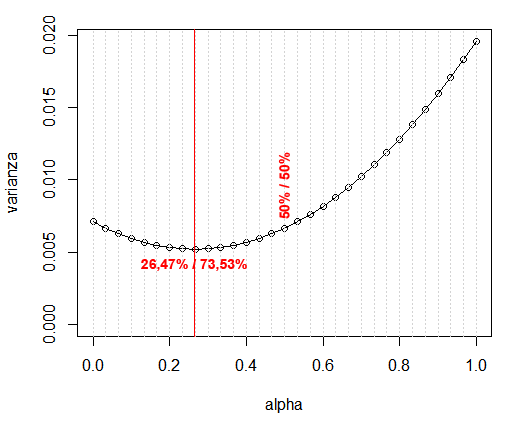
La fórmula de alpha_optimo no me la he sacado de la manga, un poco de estadística y se deduce:

Que para qué sirve esto? en aplicaciones normales para nada desde luego. Pero en programas de HDR (donde hay capturas de diferente relación S/N que hay que fusionar), o en astrofotografía donde se tiene que afinar todo lo posible puede tener aplicación. A mí me ha venido genial para practicar con un lenguaje que estoy aprendiendo.
El código:
Salu2!
No sé si se entendía del todo lo que preguntaba: no era si haciendo la media de dos capturas iguales se reduce el ruido, algo que es de sobra conocido, sino si puede reducirse el ruido aún cuando una de las 2 captura es claramente más ruidosa que la otra. Puede resultar contraintuitivo: cómo va una imagen llena de grano a ayudar a limpiar otra que está más limpia?.
La realidad es que por mucho ruido que tenga la imagen más ruidosa, siempre puede contribuir a hacer el resultado más limpio. Si la diferencia de ruido entre las dos imágenes es muy grande la contribución de la ruidosa tenderá a 0, pero nunca será nula.
He calculado que si la relación entre el ruido de las imágenes 1 y 2 es k:
Ruido_1 = k * Ruido_2 (0 < k < oo)
O dicho de otro modo, si:
Relación S/N_1 = 1/k * Relación S/N_2
La máxima mejora al fusionar ambas imágenes se consigue con un parámetro de transparencia:
alpha_optimo = 1 / (k^2 + 1) (0 < alpha_optimo < 1)
En el ejemplo que he construido con ruido gaussiano puro, la diferencia de ruido la he tomado de k=1,66666..., lo que da un alpha_optimo = 26,47% de transparencia para la imagen ruidosa, y por tanto un 73,53% para la menos ruidosa. Cuando me he llevado las imágenes a Photoshop, el cálculo ha sido casi perfecto (con ruido siempre hay una incertidumbre): para una fusión con transparencia 73% (Photoshop no deja decimales) se tiene la máxima relación S/N en la fusión; aumentando o disminuyendo empeora. La mejora no es para tirar cohetes pero menos da una piedra:

La animación muestra la imagen 1 (la más ruidosa), luego la 2 (la menos ruidosa) y por último la fusión óptima (el estrechamiento del histograma desde la imagen 2 es la contribución a la reducción del ruido de la imagen 1).
En esta gráfica puede verse que ninguna otra fusión habría dado una imagen menos ruidosa (cuando más varianza, más ruido y peor relación S/N): a la izquierda sería tomar solo la imagen 2, en el centro sería hacer una fusión 50%/50% (la habitual que hace casi todo el mundo, y que de hecho es el alpha_optimo cuando ambas imágenes tienen el mismo ruido):

La fórmula de alpha_optimo no me la he sacado de la manga, un poco de estadística y se deduce:

Que para qué sirve esto? en aplicaciones normales para nada desde luego. Pero en programas de HDR (donde hay capturas de diferente relación S/N que hay que fusionar), o en astrofotografía donde se tiene que afinar todo lo posible puede tener aplicación. A mí me ha venido genial para practicar con un lenguaje que estoy aprendiendo.
El código:
- Código: Seleccionar todo
LARGO=160000
FINE=31L
SD1=0.04*3.5
SD2=0.024*3.5
k=SD1/SD2
alphaopt=1/(k^2+1) # alpha que maximiza la S/N de la mezcla
mejora_N1=(k^2+1)^0.5
mejora_N2=(1/(k^2)+1)^0.5
S1=seq(from=0.5, to=0.5, len=LARGO)
N1=rnorm(LARGO, mean=0, sd=SD1)
S2=S1
N2=rnorm(LARGO, mean=0, sd=SD2)
# xaxis=seq(from=0, to=1, len=LARGO)
# plot(xaxis, S1+N1, ylim=c(0,1) , type='l')
# plot(xaxis, S2+N2, ylim=c(0,1) , type='l')
alpha=as.array(seq(from=0, to=1, len=FINE))
y=array(0, dim=c(FINE,LARGO))
for (i in 1:FINE) y[i,]=alpha[i]*(S1+N1)+(1-alpha[i])*(S2+N2)
yopt=alphaopt*(S1+N1)+(1-alphaopt)*(S2+N2)
varianza=alpha
for (i in 1:FINE) varianza[i]=var(y[i,])
plot(alpha, varianza, ylim=c(0,max(var(N1),var(N2))), type='o')
abline(v=alphaopt, col='red')
abline(v=alpha, col="lightgray", lty = "dotted")
# Checks
SNR1=mean(S1)/(var(N1)^0.5)
SNR2=mean(S2)/(var(N2)^0.5)
SNRopt=mean(yopt)/(var(yopt)^0.5)
print(paste0("SNRopt/SNR1=", round(SNRopt/SNR1, digits=4)," vs mejora_N1=",
round(mejora_N1,4)))
print(paste0("SNRopt/SNR2=", round(SNRopt/SNR2, digits=4)," vs mejora_N2=",
round(mejora_N2,4)))
img1=as.array(S1+N1)
img2=as.array(S2+N2)
imgout=as.array(yopt)
dim(img1) <- c(400,400) # Genialidad para convertir un vector en imagen
dim(img2) <- c(400,400)
dim(imgout) <- c(400,400)
# library(grid)
# grid.raster(imagen-min(imagen))
hist(img1, breaks=200, xlim=0:1)
img1[img1 < 0] <- 0
img2[img1 < 0] <- 0
imgout[imgout < 0] <- 0
img1[img1 > 1] <- 1
img2[img2 > 1] <- 1
imgout[imgout > 1] <- 1
library(tiff)
writeTIFF(img1, "img1.tif", bits.per.sample=16, compression="LZW")
writeTIFF(img2, "img2.tif", bits.per.sample=16, compression="LZW")
writeTIFF(imgout, "imgout.tif", bits.per.sample=16, compression="LZW")
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Ahhh vale, ahora me queda clarisimo :-p
Enviado desde Tapatalk
Enviado desde Tapatalk
SoyElTroll
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
-

soyeltroll - Mensajes: 2838
- Registrado: Lun Jul 02, 2012 12:45 am
- Ubicación: Valencia
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Ya puestos, en vez de 2 fotos, 3 mejor? 
-

Pau - Mensajes: 7450
- Registrado: Lun Dic 29, 2014 7:33 pm
- Ubicación: Vulcano
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Pau escribió:Ya puestos, en vez de 2 fotos, 3 mejor?
En astrofotografía, usando montura ecuatorial motorizada, lo habitual es hacer 20, 30, 50 o incluso 100
En esta web se puede ver la diferencia de ruido entre una única foto y 88 fotos apiladas: http://www.budgetastro.net/astrophotgra ... cking.html

-

toshiro - Mensajes: 3348
- Registrado: Vie Nov 11, 2011 1:00 pm
- Ubicación: Compostela
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Igual es una pregunta tonta pero serviria tambien fusionar copias de una misma foto?
Enviado desde mi LG-H850 mediante Tapatalk
Enviado desde mi LG-H850 mediante Tapatalk
-

arfoga - Mensajes: 1264
- Registrado: Mié Ago 15, 2012 10:24 am
- Ubicación: Alzira
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Pau escribió:Ya puestos, en vez de 2 fotos, 3 mejor?
Es que calculada la mezcla óptima para 2 fotos, puedes hacer la mezcla óptima de N fotos. Basta repetir el algoritmo con la relación S/N obtenida de la primera mezcla, por ejemplo para 3 fotos: SNR1, SNR2, SNR3
Mezclamos SNR1 y SNR2, el resultado da una SNR'
Mezclamos SNR' con SNR3
...
En relación con eso, otra aplicación de esta mezcla óptima que quise probar en su día es la obtención de BN con mínimo ruido. Un BN es la mezcla ponderada de los 3 canales RGB de la captura RAW, pero si alguno de los canales tiene mucho más ruido que los otros 2 (típicamente el azul por recibir menos exposición), lo óptimo de cara al ruido es hacer que ese canal pese menos en la mezcla. Lo tengo que probar, no me parece difícil hacer un algoritmo que genere un BN con mínimo ruido adaptándose a los niveles RGB en cada zona de la imagen, y la diferencia aquí será grande. Lo que me pregunto es qué pinta tendrá la luminosidad obtenida
toshiro escribió:En esta web se puede ver la diferencia de ruido entre una única foto y 88 fotos apiladas:
La mejora por promediar 88 fotos es 88^0,5=9,38 veces menos ruido. Para hacernos una idea de la magnitud es la misma mejora que se logra en las sombras cuando se aumenta la exposición (apertura/velocidad) en log2(9,38)=3,2EV.
arfoga escribió:Igual es una pregunta tonta pero serviria tambien fusionar copias de una misma foto?
Pues no
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Voy a decir como una mente primitiva como la mia piensa que funciona esto y me corregis si es erroneo o incompleto vale?
El ruido, en una buena proporción, aparece de forma aleatoria, si juntamos 2 fotos bastante ruidosas y comparamos los cambios es una forma facil de discernir entre lo que es ruido y lo que no, y asi generar una foto mas limpia eliminando los puntitos que no se repiten...
Enviado desde Tapatalk
El ruido, en una buena proporción, aparece de forma aleatoria, si juntamos 2 fotos bastante ruidosas y comparamos los cambios es una forma facil de discernir entre lo que es ruido y lo que no, y asi generar una foto mas limpia eliminando los puntitos que no se repiten...
Enviado desde Tapatalk
SoyElTroll
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
E-M1 + 12-40PRO + 45f1.8 + 40-150mm f4-5.6
https://www.flickr.com/photos/soyeltroll/
-

soyeltroll - Mensajes: 2838
- Registrado: Lun Jul 02, 2012 12:45 am
- Ubicación: Valencia
Re: [ENCUESTA] Ruido al mezclar dos imágenes
soyeltroll escribió:si juntamos 2 fotos bastante ruidosas y comparamos los cambios es una forma facil de discernir entre lo que es ruido y lo que no
Imagina dos imágenes monocromas de 1 píxel de resolución. En una el píxel vale 200 y en la otra vale 150.
Hala! disciérneme de manera fácil cuanto ruido tenía cada imagen
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: alpha_optimo
Guillermo Luijk escribió:Parece que ni mi voto por la opción 1 os ha disuadido de votar la opción 2
No sé si se entendía del todo lo que preguntaba: no era si haciendo la media de dos capturas iguales se reduce el ruido, algo que es de sobra conocido, sino si puede reducirse el ruido aún cuando una de las 2 captura es claramente más ruidosa que la otra. Puede resultar contraintuitivo: cómo va una imagen llena de grano a ayudar a limpiar otra que está más limpia?.
La realidad es que por mucho ruido que tenga la imagen más ruidosa, siempre puede contribuir a hacer el resultado más limpio. Si la diferencia de ruido entre las dos imágenes es muy grande la contribución de la ruidosa tenderá a 0, pero nunca será nula.
He calculado que si la relación entre el ruido de las imágenes 1 y 2 es k:
Ruido_1 = k * Ruido_2 (0 < k < oo)
O dicho de otro modo, si:
Relación S/N_1 = 1/k * Relación S/N_2
La máxima mejora al fusionar ambas imágenes se consigue con un parámetro de transparencia:
alpha_optimo = 1 / (k^2 + 1) (0 < alpha_optimo < 1)
En el ejemplo que he construido con ruido gaussiano puro, la diferencia de ruido la he tomado de k=1,66666..., lo que da un alpha_optimo = 26,47% de transparencia para la imagen ruidosa, y por tanto un 73,53% para la menos ruidosa. Cuando me he llevado las imágenes a Photoshop, el cálculo ha sido casi perfecto (con ruido siempre hay una incertidumbre): para una fusión con transparencia 73% (Photoshop no deja decimales) se tiene la máxima relación S/N en la fusión; aumentando o disminuyendo empeora. La mejora no es para tirar cohetes pero menos da una piedra:
La animación muestra la imagen 1 (la más ruidosa), luego la 2 (la menos ruidosa) y por último la fusión óptima (el estrechamiento del histograma desde la imagen 2 es la contribución a la reducción del ruido de la imagen 1).
En esta gráfica puede verse que ninguna otra fusión habría dado una imagen menos ruidosa (cuando más varianza, más ruido y peor relación S/N): a la izquierda sería tomar solo la imagen 2, en el centro sería hacer una fusión 50%/50% (la habitual que hace casi todo el mundo, y que de hecho es el alpha_optimo cuando ambas imágenes tienen el mismo ruido):
La fórmula de alpha_optimo no me la he sacado de la manga, un poco de estadística y se deduce:
Que para qué sirve esto? en aplicaciones normales para nada desde luego. Pero en programas de HDR (donde hay capturas de diferente relación S/N que hay que fusionar), o en astrofotografía donde se tiene que afinar todo lo posible puede tener aplicación. A mí me ha venido genial para practicar con un lenguaje que estoy aprendiendo.
El código:
- Código: Seleccionar todo
LARGO=160000
FINE=31L
SD1=0.04*3.5
SD2=0.024*3.5
k=SD1/SD2
alphaopt=1/(k^2+1) # alpha que maximiza la S/N de la mezcla
mejora_N1=(k^2+1)^0.5
mejora_N2=(1/(k^2)+1)^0.5
S1=seq(from=0.5, to=0.5, len=LARGO)
N1=rnorm(LARGO, mean=0, sd=SD1)
S2=S1
N2=rnorm(LARGO, mean=0, sd=SD2)
# xaxis=seq(from=0, to=1, len=LARGO)
# plot(xaxis, S1+N1, ylim=c(0,1) , type='l')
# plot(xaxis, S2+N2, ylim=c(0,1) , type='l')
alpha=as.array(seq(from=0, to=1, len=FINE))
y=array(0, dim=c(FINE,LARGO))
for (i in 1:FINE) y[i,]=alpha[i]*(S1+N1)+(1-alpha[i])*(S2+N2)
yopt=alphaopt*(S1+N1)+(1-alphaopt)*(S2+N2)
varianza=alpha
for (i in 1:FINE) varianza[i]=var(y[i,])
plot(alpha, varianza, ylim=c(0,max(var(N1),var(N2))), type='o')
abline(v=alphaopt, col='red')
abline(v=alpha, col="lightgray", lty = "dotted")
# Checks
SNR1=mean(S1)/(var(N1)^0.5)
SNR2=mean(S2)/(var(N2)^0.5)
SNRopt=mean(yopt)/(var(yopt)^0.5)
print(paste0("SNRopt/SNR1=", round(SNRopt/SNR1, digits=4)," vs mejora_N1=",
round(mejora_N1,4)))
print(paste0("SNRopt/SNR2=", round(SNRopt/SNR2, digits=4)," vs mejora_N2=",
round(mejora_N2,4)))
img1=as.array(S1+N1)
img2=as.array(S2+N2)
imgout=as.array(yopt)
dim(img1) <- c(400,400) # Genialidad para convertir un vector en imagen
dim(img2) <- c(400,400)
dim(imgout) <- c(400,400)
# library(grid)
# grid.raster(imagen-min(imagen))
hist(img1, breaks=200, xlim=0:1)
img1[img1 < 0] <- 0
img2[img1 < 0] <- 0
imgout[imgout < 0] <- 0
img1[img1 > 1] <- 1
img2[img2 > 1] <- 1
imgout[imgout > 1] <- 1
library(tiff)
writeTIFF(img1, "img1.tif", bits.per.sample=16, compression="LZW")
writeTIFF(img2, "img2.tif", bits.per.sample=16, compression="LZW")
writeTIFF(imgout, "imgout.tif", bits.per.sample=16, compression="LZW")
Salu2!
Siempre intuí que tras ese pseudónimo se escondía Sheldon Cooper
¿Acaso no es la fotografía al video lo que la poesía es a la prosa?
-

pablomaig - Mensajes: 778
- Registrado: Dom Abr 01, 2012 10:17 am
Re: [ENCUESTA] Ruido al mezclar dos imágenes
soyeltroll escribió:Voy a decir como una mente primitiva como la mia piensa que funciona esto y me corregis si es erroneo o incompleto vale?
El ruido, en una buena proporción, aparece de forma aleatoria, si juntamos 2 fotos bastante ruidosas y comparamos los cambios es una forma facil de discernir entre lo que es ruido y lo que no, y asi generar una foto mas limpia eliminando los puntitos que no se repiten...
Enviado desde Tapatalk
Eso es lo que hace si se aplica la mediana (también se puede probar promedio) en los apilamientos. Elimina lo que no se repite que puede ser ruido, o cualquier otra cosa que no permanezca constante.
-

Valdorg - Mensajes: 118
- Registrado: Lun Ago 24, 2015 2:32 pm
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Valdorg escribió:soyeltroll escribió:Voy a decir como una mente primitiva como la mia piensa que funciona esto y me corregis si es erroneo o incompleto vale?
El ruido, en una buena proporción, aparece de forma aleatoria, si juntamos 2 fotos bastante ruidosas y comparamos los cambios es una forma facil de discernir entre lo que es ruido y lo que no, y asi generar una foto mas limpia eliminando los puntitos que no se repiten...
Enviado desde Tapatalk
Eso es lo que hace si se aplica la mediana (también se puede probar promedio) en los apilamientos. Elimina lo que no se repite que puede ser ruido, o cualquier otra cosa que no permanezca constante.
La mediana y la media con dos fotos son la misma cosa
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Puesto en limpio por si a alguien le interesa el tema:
Combinación óptima de señales para minimizar ruido con R
Salu2!
Combinación óptima de señales para minimizar ruido con R
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Aplicación: BN con mínimo ruido
Con la idea de aplicar el algoritmo a la construcción de un BN basado en el RAW con mínimo ruido, he extendido el cálculo a la combinación de 3 señales (canales RGB):


Una primera prueba (el algoritmo es mejorable, de momento he asumido que todo el ruido es de lectura, pero para ruido fotónico la mezcla óptima varía) aplicando esos 3 pesos a los canales de una extracción RAW pura (la comparo con otros métodos conocidos):
ALGORITMO ÓPTIMO

CAPA DE AJUSTE DE BN DE PHOTOSHOP

CONVERSIÓN A LAB

ESCALA DE GRISES

Curiosamente este último método que suele ser desechado, en cuanto a ruido es el que más se acerca al algoritmo óptimo (algo que ya me había dado la impresión en el pasado), pero el algoritmo óptimo los supera a todos.
Esta imagen da una idea de por dónde han ido los tiros en la fusión de los 3 canales RAW, se trata de una imagen virtual que nos indica en cada zona la participación relativa que ha tenido cada canal en la construcción del BN. Puede verse que el canal azul, que generalmente tiene menos exposición y por tanto peor relación S/N que los otros dos, solo es dominante en la cabina de Koji Kabuto y en ciertas áreas de las sombras profundas que son azuladas:

La cabina relativamente pobre en rojos y verdes tiene mucho menos ruido en la combinación óptima que en cualquiera de los otros métodos. También ocurre esto en las zonas rojas del pecho de Mazinger. En general intuyo que el algoritmo mejorará más a los métodos tradicionales en zonas atípicas donde el canal verde del RAW no sea dominante. Voy a probar con un RAW infrarrojo que tengo por algún lado.
Salu2!


Una primera prueba (el algoritmo es mejorable, de momento he asumido que todo el ruido es de lectura, pero para ruido fotónico la mezcla óptima varía) aplicando esos 3 pesos a los canales de una extracción RAW pura (la comparo con otros métodos conocidos):
ALGORITMO ÓPTIMO

CAPA DE AJUSTE DE BN DE PHOTOSHOP

CONVERSIÓN A LAB

ESCALA DE GRISES

Curiosamente este último método que suele ser desechado, en cuanto a ruido es el que más se acerca al algoritmo óptimo (algo que ya me había dado la impresión en el pasado), pero el algoritmo óptimo los supera a todos.
Esta imagen da una idea de por dónde han ido los tiros en la fusión de los 3 canales RAW, se trata de una imagen virtual que nos indica en cada zona la participación relativa que ha tenido cada canal en la construcción del BN. Puede verse que el canal azul, que generalmente tiene menos exposición y por tanto peor relación S/N que los otros dos, solo es dominante en la cabina de Koji Kabuto y en ciertas áreas de las sombras profundas que son azuladas:

La cabina relativamente pobre en rojos y verdes tiene mucho menos ruido en la combinación óptima que en cualquiera de los otros métodos. También ocurre esto en las zonas rojas del pecho de Mazinger. En general intuyo que el algoritmo mejorará más a los métodos tradicionales en zonas atípicas donde el canal verde del RAW no sea dominante. Voy a probar con un RAW infrarrojo que tengo por algún lado.
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Comparación con Capa de Ajuste de BN de Photoshop (Preset = None):

Salu2!

Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Aqui sigo leyendote para seguir aprendiendo. Muchisimas gracias por compartir tu conocimiento!
-

ssantos77 - Mensajes: 49
- Registrado: Lun Jun 13, 2016 11:42 am
- Ubicación: Leganés (Madrid)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Cuando activamos la reducción de ruido por largas exposiciones en la cámara, esta tarda el doble de tiempo en procesar la imagen, ya que genera una imagen "en negro" y la mezcla con las zonas donde ha generado ruido la foto.
Es la misma "base" que mezclar estas 2 fotos que comentas?
Enviado desde mi CUBOT ECHO mediante Tapatalk
Es la misma "base" que mezclar estas 2 fotos que comentas?
Enviado desde mi CUBOT ECHO mediante Tapatalk
https://www.flickr.com/photos/30032076@N02/
Olympus E-M10 - Olympus E-M1II - Laowa 7.5mm f2 - Panasonic 20mm 1.7 - Panasonic 12-32mm - Zuiko 40-150 2.8
Olympus E-M10 - Olympus E-M1II - Laowa 7.5mm f2 - Panasonic 20mm 1.7 - Panasonic 12-32mm - Zuiko 40-150 2.8
-

danixmen - Mensajes: 718
- Registrado: Jue Nov 05, 2015 11:03 am
- Ubicación: Algeciras
Re: [ENCUESTA] Ruido al mezclar dos imágenes
No tiene nada que ver. Esa reducción de ruido es una resta para que los niveles RAW anómalos (hotpixels y ruido espacial en general, es decir el que aparece en igual localización y amplitud en todas las tomas), se cancele.
Aquí lo que he calculado es en qué % debe aparecer cada imagen origen en el resultado final para que el ruido sea mínimo.
Si tienes dos imágenes de igual exposición el peso será 50%/50%. Si son de diferente exposición los pesos serán distintos (me lo invento: 70% para la más y 30% para la menos expuesta).
Salu2!
Aquí lo que he calculado es en qué % debe aparecer cada imagen origen en el resultado final para que el ruido sea mínimo.
Si tienes dos imágenes de igual exposición el peso será 50%/50%. Si son de diferente exposición los pesos serán distintos (me lo invento: 70% para la más y 30% para la menos expuesta).
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Entiendo (o creo)....y si fuera una foto tan subexpuestas que fuera casi oscura, digamos que el peso fuera 99%-1%? Supongo que entonces apenas se reduciría el ruido
Enviado desde mi CUBOT ECHO mediante Tapatalk
Enviado desde mi CUBOT ECHO mediante Tapatalk
https://www.flickr.com/photos/30032076@N02/
Olympus E-M10 - Olympus E-M1II - Laowa 7.5mm f2 - Panasonic 20mm 1.7 - Panasonic 12-32mm - Zuiko 40-150 2.8
Olympus E-M10 - Olympus E-M1II - Laowa 7.5mm f2 - Panasonic 20mm 1.7 - Panasonic 12-32mm - Zuiko 40-150 2.8
-

danixmen - Mensajes: 718
- Registrado: Jue Nov 05, 2015 11:03 am
- Ubicación: Algeciras
Re: [ENCUESTA] Ruido al mezclar dos imágenes
Claro, en ese caso el resultado sería equivalente a tomar la captura mejor expuesta y desechar la otra.
Salu2!
Salu2!
Último contenido: PROFUNDIDAD DE CAMPO TRAS HACER "ZOOM DIGITAL"
-

Guillermo Luijk - Mensajes: 9830
- Registrado: Dom Ene 31, 2010 6:37 am
- Ubicación: Madrid (a ratos Alicante)
25 mensajes
• Página 1 de 1
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 2 invitados