El caso es que además de todo llevan un filtro para pantallas que evita las frecuencias supuestamente más dañinas (los azules), pero este filtro genera una dominante cálida claramente visible que echa por tierra cualquier calibración precisa de la pantalla, así que para editar fotos de forma ortodoxa como que no.
El caso es que he querido cuantifcar la desviación mirando de la forma lo más neutra posible cuanto se mueven los niveles RGB sin y con gafas. He hecho una foto a una pantalla blanca sin/con las gafas delante de la óptica, y usado el balance de blancos que la deja 100% neutra en las dos tomas.
Al hacer balance de blancos en el centro de las capturas se tiene una diferencia de 150 K:
- Sin gafas: 4550 K, Matiz +8
- Con gafas: 4400 K, Matiz +11
He hecho la conversión a sRGB (podría haberlo hecho en el dominio RAW, pero he creido que es mejor convertir porque los valores RGB obtenidos son más cercanos a los valores numéricos a los que estamos acostumbrados), y comparado los histogramas:
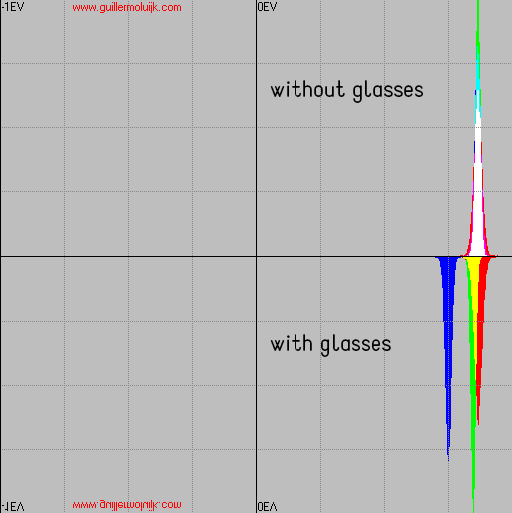
Las diferencias son tan sutiles que incluso con ese nivel de zoom (la gráfica anterior abarca solo 2 pasos de exposición) se hace complicado cuantificar. Así que he hecho el cálculo numéricamente y dibujado los histogramas con zoom, tomando como referencia los canales de la primera captura (exp. relativa=1):
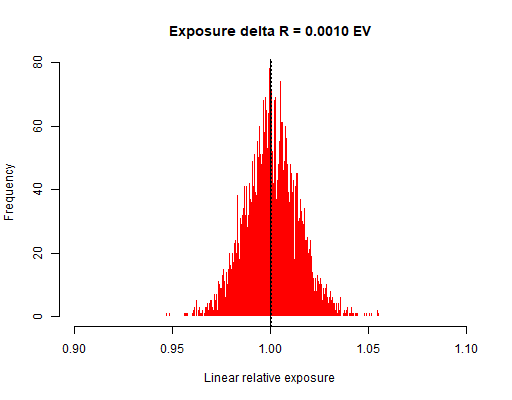
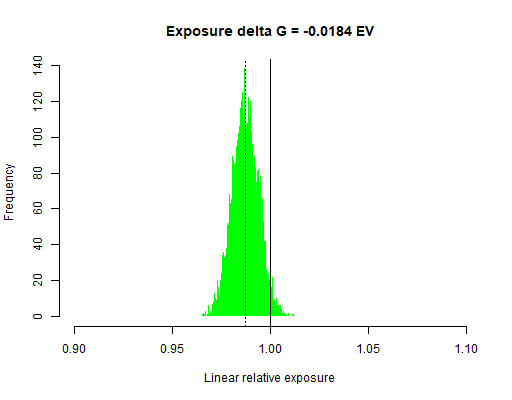
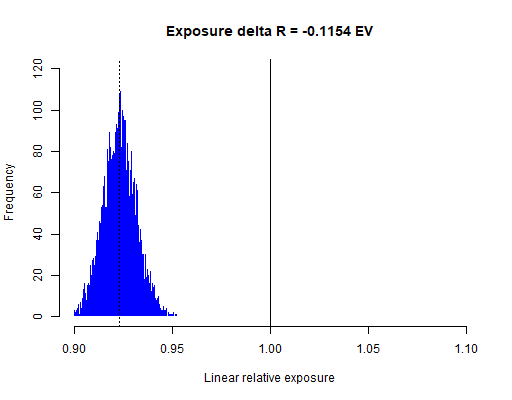
El valor del canal R apenas se mueve, el G pierde 0,018 EV pasos y el B 0,115 EV pasos, que son los causantes del tono cálido.
Aquí es como se ven los parches analizados (para toda la prueba se ha tomado un parche central de 100x100 píxeles) sin y con las gafas y el balance de blancos aplicado:

La anchura de las campanas de Gauss se debe exclusivamente al ruido fotónico, ya que al ser capturas muy derecheadas el ruido electrónico no es apreciable. El canal más ruidoso (menor exposición en el RAW) en este caso fue el rojo, de ahí la mayor a anchura de su histograma.
Salu2!